6. 숫자 데이터 타입 사용하기
프로그래밍을 하다보면 정수 및 실수 데이터를 자주 사용합니다. 이번 강의는 숫자 데이터 타입에 대해서 알아보는 시간을 갖습니다.
> // 숫자 데이터 타입: int, long, float, double 등의 키워드로 숫자 데이터 저장
NOTE
데이터 형식(Type)이 가장 기본적인 표현 방법이지만, 데이터 형식, 데이터 유형, 자료형 등으로 표현되는 방법에 대한 차이를 줄이기 위해서 Type을 타입으로 표현하도록 하겠습니다. 박용준 강사의 강의에서 데이터 타입은 데이터 형식을 단어 그대로 표현한 것 뿐입니다.
이진수의 이해: 컴퓨터 언어의 기본
이진수는 모든 현대 컴퓨터 및 디지털 시스템의 기반이 되는 숫자 체계입니다. 이 아티클에서는 이진수가 무엇인지, 왜 중요한지, 그리고 어떻게 사용되는지에 대해 알아보겠습니다.
이진수란 무엇인가?
이진수는 0과 1 두 가지 숫자만을 사용하는 진법 체계입니다. 이는 10진수 체계에서 사용하는 0부터 9까지의 숫자와는 다릅니다. 이진수에서 각 자리는 '비트'(bit)라고 불리며, 각 비트는 전기적 신호의 상태를 표현할 수 있습니다—0은 꺼짐(off), 1은 켜짐(on)을 의미합니다.
이진수의 중요성
이진수는 컴퓨터 하드웨어와 소프트웨어 양쪽 모두에서 기본적인 언어로 사용됩니다. 컴퓨터는 내부적으로 이진수를 사용하여 데이터를 저장하고 처리합니다. 이러한 이유로, 모든 프로그래밍 언어와 운영 체제, 응용 프로그램은 궁극적으로 이진수를 사용하여 컴퓨터와 통신합니다.
이진수 사용 예
데이터 저장과 처리: 컴퓨터는 텍스트, 이미지, 비디오 등 모든 형태의 데이터를 이진 형식으로 저장합니다. 예를 들어, 문자는 ASCII 코드를 사용하여 이진 숫자로 변환되어 저장됩니다.
논리 연산: 컴퓨터는 이진 논리 연산(AND, OR, NOT 등)을 사용하여 계산을 수행합니다. 이러한 연산은 컴퓨터 프로세서 내의 트랜지스터 수준에서 이루어지며, 이는 모든 프로그램 실행의 기본을 형성합니다.
네트워킹: 컴퓨터 네트워크에서 데이터 전송도 이진 형태로 이루어집니다. 예를 들어, 인터넷을 통해 보내는 데이터 패킷은 이진 코드로 인코딩되어 전송됩니다.
이진수의 장점
이진수 시스템은 그 간결성과 오류 감지 및 수정이 용이하다는 점에서 매우 효율적입니다. 또한, 이진수는 물리적으로 신뢰성이 높은 전자 부품을 사용하여 쉽게 표현되고 조작될 수 있습니다.
10진수와 2진수 변환 가이드
이 아티클에서는 양수에 한정하여 10진수를 2진수로 변환하는 방법과 그 반대의 과정을 단계별로 설명하겠습니다.
10진수를 2진수로 변환하기
10진수를 2진수로 변환하는 과정은 다음과 같습니다:
- 나눗셈과 나머지: 주어진 10진수를 2로 나누고, 나머지를 기록합니다. 이 과정을 수가 0이 될 때까지 반복합니다.
- 결과 기록: 마지막 나머지부터 첫 번째 나머지까지 역순으로 기록합니다. 이렇게 하면 해당 10진수의 2진 표현이 완성됩니다.
예제: 10진수 156을 2진수로 변환하기
- (156 / 2 = 78) 나머지 0
- (78 / 2 = 39) 나머지 0
- (39 / 2 = 19) 나머지 1
- (19 / 2 = 9) 나머지 1
- (9 / 2 = 4) 나머지 1
- (4 / 2 = 2) 나머지 0
- (2 / 2 = 1) 나머지 0
- (1 / 2 = 0) 나머지 1
역순으로 나머지를 읽으면 156의 2진수는 (10011100)입니다.
2진수를 10진수로 변환하기
2진수를 10진수로 변환하는 방법은 다음과 같습니다:
- 가중치 적용: 2진수의 각 자리수에 가중치를 적용합니다. 가장 오른쪽 자리부터 시작하여, 각 자리의 가중치는 (2^0, 2^1, 2^2, ...)와 같이 증가합니다.
- 합산: 모든 자리의 가중치가 적용된 값을 합산합니다.
예제: 2진수 10011100을 10진수로 변환하기
- (0 * 2^0 = 0)
- (0 * 2^1 = 0)
- (1 * 2^2 = 4)
- (1 * 2^3 = 8)
- (1 * 2^4 = 16)
- (0 * 2^5 = 0)
- (0 * 2^6 = 0)
- (1 * 2^7 = 128)
모든 값을 합하면 (128 + 16 + 8 + 4 = 156).
음수의 2진수 표현: -45를 2진수로 변환하기
2진수는 컴퓨터가 정보를 처리하고 저장하는 기본 방식으로, 양의 정수뿐만 아니라 음의 정수를 표현하는 데에도 사용됩니다. 이 글에서는 -45라는 음수를 2진수로 변환하는 과정을 단계별로 설명하겠습니다.
1. 절댓값 구하기
음수의 2진수 변환을 시작하기 전에, 먼저 해당 숫자의 절댓값을 구해야 합니다. -45의 절댓값은 45입니다.
2. 45를 2진수로 변환하기
45를 2진수로 변환하기 위해 2로 나누는 과정을 반복하고, 각 단계에서의 나머지를 기록합니다.
- ( 45 / 2 = 22 ) 나머지 1
- ( 22 / 2 = 11 ) 나머지 0
- ( 11 / 2 = 5 ) 나머지 1
- ( 5 / 2 = 2 ) 나머지 1
- ( 2 / 2 = 1 ) 나머지 0
- ( 1 / 2 = 0 ) 나머지 1
이 나머지들을 거꾸로 읽으면 45의 2진수는 (101101)입니다.
3. 2의 보수 구하기
음수를 표현하기 위해서는 2의 보수를 사용합니다. 이를 구하는 과정은 먼저 1의 보수를 취한 다음, 1을 더하는 것입니다.
1의 보수는 각 비트를 반전시키는 것으로, 45의 2진수 (101101)의 1의 보수는 (010010)입니다. 이제 여기에 1을 더합니다:
- (010010 + 1 = 010011)
4. 8비트로 확장하기
일반적으로 컴퓨터 시스템은 8비트, 16비트 등으로 비트를 표준화하여 사용합니다. 여기서는 8비트를 사용한다고 가정하고, 45의 2진수를 확장해 보겠습니다.
- 45의 2진수를 8비트로 확장: (00101101)
- 1의 보수 (8비트): (11010010)
- 2의 보수 (1의 보수에 1 더하기): (11010011)
따라서, -45의 2진수 표현 (8비트 2의 보수 방식)은 (11010011)입니다.
음수 이진수를 10진수로 변환: 1101 0110을 10진수로 변환하기
이 글에서는 8비트 이진수 "1101 0110"을 예로 들어 음수 표현 방식을 단계별로 설명하겠습니다.
1. 이진수 이해하기
8비트 이진수에서 첫 번째 비트는 부호 비트로, 이는 숫자의 양수/음수 여부를 나타냅니다. 부호 비트가 0이면 양수, 1이면 음수를 의미합니다. 여기서는 "1101 0110"의 첫 비트가 1이므로 이는 음수를 표현합니다.
2. 2의 보수로 변환
음수를 10진수로 바로 변환하려면 먼저 2의 보수를 계산해야 합니다. 2의 보수를 구하는 과정은 다음과 같습니다.
1의 보수 구하기
모든 비트를 반전시켜 1의 보수를 얻습니다.
- 원래 값: 1101 0110
- 1의 보수: 0010 1001
2의 보수 구하기
1의 보수에 1을 더해 2의 보수를 구합니다.
- 1의 보수: 0010 1001
- 1 더하기: 0010 1010
3. 2의 보수를 10진수로 변환
이제 2의 보수를 10진수로 변환하여 실제 수치를 얻습니다.
- 2의 보수: 0010 1010
- 0 * 2^7 = 0
- 0 * 2^6 = 0
- 1 * 2^5 = 32
- 0 * 2^4 = 0
- 1 * 2^3 = 8
- 0 * 2^2 = 0
- 1 * 2^1 = 2
- 0 * 2^0 = 0
합계: 32 + 8 + 2 = 42
부호 비트가 1이므로, 이 수는 -42입니다.
6.1. 숫자 데이터 타입
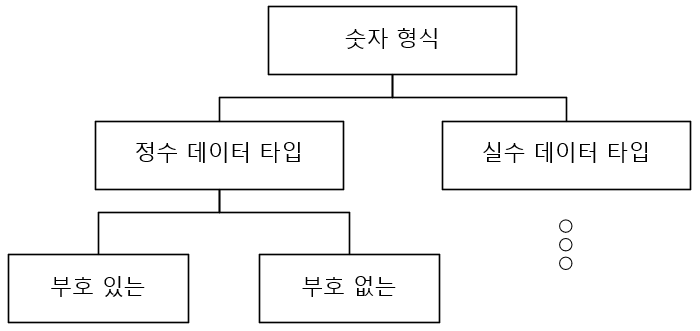
C 언어에서는 숫자 형식의 데이터를 다룰 때 사용되는 int 키워드를 포함하여 여러 가지 키워드를 제공합니다. 숫자 데이터 타입은 크게 정수 데이터 타입과 소수점을 가지는 실수 데이터 타입이 있습니다. 정수 데이터 타입 중에는 다시 부호 있는 숫자와 부호 없는 숫자로 나눕니다.
그림: 숫자 형식
NOTE
많은 종류의 숫자 관련 데이터 타입은 long double > double > float > unsigned long > long > unsigned int > int > unsigned char > char 형태로 더 큰 수를 담을 수 있습니다.
정수 리터럴
정수 형식을 표현할 때 정수 리터럴을 사용할 수 있습니다. 기본 숫자만 사용하면 10진수로 표현되고, 숫자 앞에 0x(Zero X)를 붙이면 16진수, 0(Zero) 하나만 붙이면 8진수로 표현됩니다.
코드: number_literal.c
// 정수 리터럴
#include <stdio.h>
int main(void)
{
printf("%d\n", 1234); // 10진수
printf("%d\n", 0x1234); // 16진수
printf("%d\n", 01234); // 8진수
return 0;
}
1234
4660
668
출력 결과는 10진수 1234와 16진수 1234가 10진수로 변환된 4660과 8진수 1234가 10진수로 변환된 668이 출력됩니다. 참고로, 진법 변환에 대한 내용은 이 강의에서는 따로 다루지는 않습니다. (필요하다면 Windows에 내장된 계산기(calc)의 프로그래머 옵션을 사용하세요.)
6.2. 정수 데이터 타입 사용하기
정수형 키워드에는 signed와 unsigned 키워드가 붙는데, 둘의 차이점은 signed와 unsigned의 영어 단어 의미 그대로인 부호가 붙느냐 안 붙느냐의 차이점입니다.
- 부호 있는(
signed): +, - 부호가 있는 정수형입니다. 즉, 양수와 음수를 모두 지원합니다. - 부호 없는(
unsigned): 부호 없이 + 값만을 다루는 정수형입니다. 즉 양수만을 지원합니다.
정수 데이터 타입의 종류는 다음 표를 참고하세요.
표: 정수 데이터 타입의 종류
| 종류 | 키워드 |
|---|---|
| 정수 데이터 타입 | char |
| int | |
| long, long long | |
| 부호 있는 정수(+, -) | char |
| short | |
| int, long, long long | |
| 부호 없는 정수(+) | unsigned short |
| unsigned int | |
| unsigned long | |
| unsigned long long |
참고로, 표의 char 키워드는 정수를 담을 수도 있지만, 강의에서는 문자 하나를 담는 역할로만 사용합니다.
6.3. 정수형 변수 선언하고 초기화하기
앞서, 변수 사용하기를 공부할 때 이미 int 키워드를 사용하여 정수형 변수를 선언하는 방법을 사용했었는데요. 이번에는 정수형 변수가 가질 수 있는 최솟값과 최댓값을 직접 저장한 후 출력하는 예제를 만들어보겠습니다.
코드: integer_demo.c
#include <stdio.h>
int main(void)
{
int min = -2147483647 - 1; // 정수형이 가질 수 있는 가장 작은값
int max = +2147483647; // 정수형이 가질 수 있는 가장 큰값
printf("int 변수의 최솟값: %d\n", min); // int 변수의 최솟값: -2147483648
printf("int 변수의 최댓값: %d\n", max); // int 변수의 최댓값: 2147483647
return 0;
}
int 변수의 최솟값: -2147483648
int 변수의 최댓값: 2147483647
int 키워드를 사용한 정수형은 최소 -21억부터 최대 +21억까지의 데이터를 저장하는 데 사용됩니다. 위 예제에서 실행된 결과값을 외울 필요는 없습니다.
참고로, int 형식은 대부분 컴퓨터에서 4 바이트(32 비트)로 처리됩니다. 그래서, 2의 32제곱을 반으로 나눠서 마이너스 값과 0을 포함한 플러스 값을 담을 수 있는 공간인 -21억부터 +21억까지의 수를 나타냅니다.
6.4. 부호(+, -) 있는 정수 데이터 타입
C 언어에는 +와 -의 정수를 다룰 수 있는 데이터 타입을 제공합니다. short, int, long, long long 순서대로 작은 수부터 큰 정수까지 담아놓을 수 있습니다. 프로그래밍 환경마다 다를 수 있지만 기본적으로 short는 16비트, int는 32비트, long은 32비트, long long은 64비트 크기의 저장소를 사용하여 부호 있는 정수를 담을 수 있습니다.
부호 있는 정수 데이터 타입의 범위는 다음 그림과 같습니다. 값의 범위를 외우거나 상세히 기억할 필요는 전혀 없으니 간단히 살펴보고 넘어가면 됩니다.
그림: 부호 있는 정수의 범위

참고: C 언어 데이터 타입
6.5. 부호 있는 정수 데이터 타입 사용하기
부호 있는 정수 데이터 타입의 4가지 키워드를 사용해보는 예제를 작성해 보겠습니다.
코드: signed_integer.c
// 부호(+, -) 있는 정수 데이터 형식: short, int, long, long long
#include <stdio.h>
int main(void)
{
//[1] 부호 있는 정수 데이터 형식 변수 선언
short s = 32767; // 16비트 부호 있는 정수형 변수 선언 및 할당
int i = 2147483647; // 32비트 부호 있는 정수형 변수 선언 및 할당
long l = 2147483647; // 32비트 부호 있는 정수형 변수 선언 및 할당
long long ll = 9223372036854775807; // 64비트 부호 있는 정수형 변수 선언 및 할당
//[2] 서식 지정자(자리 표시자): short(%d), int(%d), long(%ld), long long(%lld)
printf("short: %d\n", s); // short: 32767
printf("int: %d\n", i); // int: 2147483647
printf("long: %ld\n", l); // long: 2147483647
printf("long long: %lld\n", ll); // long long: 9223372036854775807
return 0;
}
short: 32767
int: 2147483647
long: 2147483647
long long: 9223372036854775807
실행 결과는 short, int, long, long long 키워드로 선언된 변수가 가질 수 있는 가장 큰 값을 넣은 후 출력하는 내용입니다.
6.6. 부호 있는 데이터 타입 사용하기
부호 있는 데이터 타입의 크기와 최댓값 그리고 최솟값을 출력해보도록 하겠습니다. 다음 코드 안의 숫자 값은 직접 작성해도 되지만 복사해서 사용해도 됩니다.
코드: integer_type.c
// 부호 있는 정수 데이터 타입 사용하기
#include <stdio.h>
#include <limits.h> // 정수 데이터 타입의 최댓값과 최솟값에 대한 상수 정의
int main(void)
{
//[1] 정수 데이터 타입 변수 선언
short s = 32767;
int i = 2147483647;
long l = 2147483647;
long long ll = 9223372036854775807;
//[2] 자리 표시자: short(%d), int(%d), long(%ld), long long(%lld)
//32767 2147483647 2147483647 9223372036854775807
printf("%d %d %ld %lld\n", s, i, l, ll);
//[3] 정수 데이터 타입 크기: sizeof로 데이터 타입 크기를 알 수 있고 %llu로 출력
// 리눅스 환경의 GCC 컴파일러에서는 서식 지정자로 %llu 대신에 %lu로 출력해야 함
printf("%llu %llu %llu %llu\n",
sizeof(short), // 2
sizeof(int), // 4
sizeof(long), // 4
sizeof(long long) // 8
);
//[4] 정수 데이터 타입의 범위: 큰 숫자이므로 지수 표기법으로 출력
//short: -32768 ~32767
printf("short: %d ~ %d\n", SHRT_MIN, SHRT_MAX);
//int : -2147483648 ~2147483647
printf("int: %d ~ %d\n", INT_MIN, INT_MAX);
//long : -2147483648 ~2147483647
printf("long: %ld ~ %ld\n", LONG_MIN, LONG_MAX);
//long long : -9223372036854775808 ~9223372036854775807
printf("long long: %lld ~ %lld\n", LLONG_MIN, LLONG_MAX);
return 0;
}
32767 2147483647 2147483647 9223372036854775807
2 4 4 8
short: -32768 ~ 32767
int: -2147483648 ~ 2147483647
long: -2147483648 ~ 2147483647
long long: -9223372036854775808 ~ 9223372036854775807
- [1] 정수 데이터 타입은 각각
short,int,long,long long키워드를 사용하여 데이터를 저장합니다. 이 때 정수 데이터는int키워드를 가장 많이 사용합니다. - [2] 정수 데이터 타입 출력에 대한 서식 지정자는
short와int는%d,long은%ld,long long은%lld를 사용합니다. - [3] sizeof() 연산자라는 것을 통해서 정수 데이터 타입의 크기를 구할 수가 있습니다. 여기서 주의할 것은 데이터 타입의 크기는 운영체제마다 다를 수 있습니다.
- [4] limits.h 이름의 헤더 파일에는 정수 데이터 형식의 최댓값과 최솟값을 담고 있는 상수가 정의되어 있습니다.
SHRT_MIN,SHRT_MAX,INT_MIN,INT_MAX,LONG_MIN,LONG_MAX,LLONG_MIN,LLONG_MAX의 6개 상수로short,int,long,long long의 최댓값과 최솟값을 알 수 있습니다. 이것도 마찬가지로 운영체제마다 다를 수 있습니다.
| 데이터 타입 | 최솟값 | 최댓값 |
|---|---|---|
| short | SHRT_MIN | SHRT_MAX |
| int | INT_MIN | INT_MAX |
| long | LONG_MIN | LONG_MAX |
| long long | LLONG_MIN | LLONG_MAX |
6.7. 부호 없는 정수 데이터 타입
부호 없는 정수 데이터 타입은 - 값을 사용할 수 없지만, + 값을 부호 있는 정수 타입의 2배 크기로 사용할 수 있는 데이터 타입을 제공합니다. 부호 없는 정수 데이터 타입은 unsigned short, unsigned int, unsigned long, unsigned long long의 4가지를 사용합니다. 각각의 범위는 다음 그림과 같이 부호 있는 범위보다 2배 더 큰 양의 정수 값을 제공합니다.
그림: 부호 없는 정수의 범위

부호 없는 데이터 타입을 사용해보겠습니다.
코드: unsigned_integer_type.c
// 부호 없는 정수 데이터 타입 사용하기
#include <stdio.h>
#include <limits.h> // 정수 데이터 타입의 최댓값과 최솟값에 대한 상수 정의
int main(void)
{
//[1] 정수 데이터 타입 변수 선언
unsigned short s = 65535;
unsigned int i = 4294967295;
unsigned long l = 4294967295;
unsigned long long ll = 18446744073709551615;
//[2] 자리 표시자: short(%u), int(%u), long(%lu), long long(%llu)
printf("%u %u %lu %llu\n", s, i, l, ll); //
//[3] 정수 데이터 타입 크기: sizeof로 데이터 타입 크기를 알 수 있고 %llu로 출력
// 리눅스 환경의 GCC 컴파일러에서는 서식 지정자로 %llu 대신에 %lu로 출력해야 함
printf("%llu %llu %llu %llu\n",
sizeof(unsigned short),
sizeof(unsigned int),
sizeof(unsigned long),
sizeof(unsigned long long)
);
//[4] 정수 데이터 타입의 범위
printf("unsigned short: 0 ~ %u\n", USHRT_MAX);
printf("unsigned int: 0 ~ %u\n", UINT_MAX);
printf("unsigned long: 0 ~ %lu\n", ULONG_MAX);
printf("unsigned long long: 0 ~ %llu\n", ULLONG_MAX);
return 0;
}
65535 4294967295 4294967295 18446744073709551615
2 4 4 8
unsigned short: 0 ~ 65535
unsigned int: 0 ~ 4294967295
unsigned long: 0 ~ 4294967295
unsigned long long: 0 ~ 18446744073709551615
위 코드는 unsigned short, unsigned int, unsigned long, unsigned long long 키워드로 선언된 변수가 가질 수 있는 가장 큰 값을 넣은 후 출력하는 내용입니다. 부호 있는 정수형보다 2배 큰 범위의 값을 넣을 수 있습니다.
6.8. 정수 데이터 타입의 크기
sizeof() 연산자를 사용하여 주요 정수 데이터 타입의 크기를 바이트 단위로 표현할 수 있습니다. sizeof() 연산자의 결괏값은 %lld 서식 지정자를 사용하여 출력합니다.
관련 강의
코드: integer_size.c
// 정수 데이터 형식의 크기
#include <stdio.h>
int main(void)
{
printf("short: %lld\n", sizeof(short)); // short: 2
printf("int: %lld\n", sizeof(int)); // int: 4
printf("long: %lld\n", sizeof(long)); // long: 4
printf("unsigned: %lld\n", sizeof(unsigned)); // unsigned: 4
return 0;
}
short: 2
int: 4
long: 4
unsigned: 4
위 소스의 내용은 실제로는 다음 서식 지정자를 사용하는 걸 권장합니다.
| 자료형 | 서식 지정자 |
|---|---|
| short | %hd 또는 %hi |
| int | %d |
| long | %ld |
| long long | %lld |
stdint.h는 C99 표준에서 추가된 헤더 파일 중 하나로, 정수형 데이터의 크기와 부호 여부를 명시적으로 지정하는 데 사용됩니다. 이 헤더 파일은 다양한 운영 체제와 아키텍처에서 코드의 이식성을 높이기 위해 사용됩니다.
stdint.h 헤더 파일은 다음과 같은 데이터 형식을 정의합니다.
- int8_t : 부호 있는 8비트 정수형
- uint8_t : 부호 없는 8비트 정수형
- int16_t : 부호 있는 16비트 정수형
- uint16_t : 부호 없는 16비트 정수형
- int32_t : 부호 있는 32비트 정수형
- uint32_t : 부호 없는 32비트 정수형
- int64_t : 부호 있는 64비트 정수형
- uint64_t : 부호 없는 64비트 정수형
이러한 데이터 형식은 특정 크기와 부호를 갖기 때문에 코드 이식성을 향상시키고, 정확한 데이터 형식이 필요한 경우에 사용됩니다.
또한, int_leastN_t와 uint_leastN_t 형식도 제공됩니다. 이 형식은 적어도 N비트의 크기를 보장합니다. 예를 들어, int_least16_t는 16비트 이상의 크기를 보장합니다.
마지막으로, intmax_t와 uintmax_t는 정수형 데이터 중 가장 큰 크기를 갖습니다. 이러한 형식은 매우 큰 정수 값을 처리해야 하는 경우에 사용됩니다.
6.9. 오버플로(Overflow)
int 형식이 담을 수 있는 범위를 벗어나는 데이터로 초기화되면 이를 오버플로(overflow)라고 해서 잘못된 데이터가 담깁니다. 그래서 프로그래밍할 때에는 데이터 타입의 범위를 확인하면서 코드를 작성해야 합니다. 예를 들어 int 타입이 저장할 수 있는 범위를 벗어나는 다음 코드의 실행 결과는 잘못된 데이터입니다.

코드: integer_overflow.c
int num = (2147483647 + 2147483647); // INT_MAX + INT_MAX
printf("%d\n", num); // 잘못된 데이터 값 출력
-2
코드: integer_overflow.c
int 형식이 담을 수 있는 범위를 벗어나는 데이터로 초기화되면 오버플로에 의해서 잘못된 데이터가 담깁니다. 그래서 프로그래밍할 때에는 데이터 타입의 범위를 확인하면서 코드를 작성해야 합니다.
// integer_overflow.c
#include <stdio.h>
// limits.h 헤더 파일의 INT_MAX, INT_MIN으로 정수 형식의 최댓값, 최솟값 알 수 있음
// #include <limits.h>
int main(void)
{
// int 형식의 범위: -2147483648 ~ +2147483647
// 담을 수 있는 범위를 벗어남: 오버플로(넘침) 발생
int num = (2147483647 + 2147483647); // INT_MAX + INT_MAX
printf("%d\n", num); // 잘못된 데이터 값 출력
return 0;
}
실행
-2
6.10. 실수 데이터 타입 사용하기
소수점 이하의 숫자를 다루는 실수 데이터 타입(부동 소수점(Floating Point) 데이터 타입)에 대해서 살펴보겠습니다. 부동 소수점 데이터 타입으로 표현되는 실수를 컴퓨터에서 표현하는 방법은 복잡합니다. 이러한 표현 방법에 대해서 설명하는 것은 박용준 강사의 이 강의의 범위를 벗어나기에 실수 데이터 타입은 3.14와 같이 우리가 평상시에 사용하던 방식의 실수 그 자체로 이해하면 됩니다.
실수 데이터는 부동 소수점 방식의 데이터 타입인 float, double, long double 키워드를 제공합니다.
그림: 실수 데이터 타입
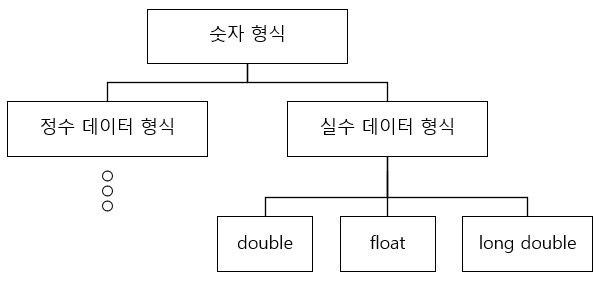
Windows 운영체제를 기준으로 실수 데이터 타입을 나타내는 double은 64비트, float는 32비트, long double은 64비트의 크기를 갖습니다.
실수 데이터 타입의 종류는 다음 표와 같습니다. 너무 어렵게 생각할 필요없이 float, double, long double 키워드가 실수 데이터를 표현한다는 것만 기억하면 됩니다.
표: 실수 데이터 타입의 종류(Windows 기준)
| 종류 | 키워드 | 크기 | 비고 |
|---|---|---|---|
| 부동 소수점 방식 | float | 4바이트 | IEEE 754 단정밀도 부동 소수점 |
| double | 8바이트 | IEEE 754 배정밀도 부동 소수점 | |
| long double | 8바이트 | IEEE 754 배정밀도 부동 소수점 |
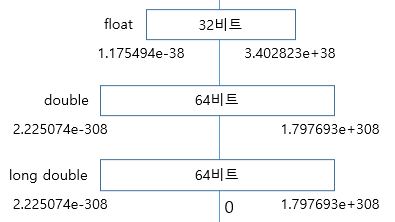
실수 데이터 타입이 갖는 크기와 값의 범위는 다음 그림과 같습니다. 정수 데이터 타입과 마찬가지로 여기에 나오는 값들의 크기와 범위는 외울 필요는 없습니다. 필요할 때 다시 찾아보면 됩니다. 아래 표기법은 지수 표기법으로 표현했는데 float 데이터 타입의 최댓값은 약 3.4 곱하기 10의 38제곱 정도로 볼 수 있습니다.
그림: 실수 데이터 타입의 범위(Windows 기준)
6.10.1. 참고: 지수 표기법
아주 큰 수와 아주 작은 수를 표현할 때에는 지수 표기법(Exponential Notation)을 사용합니다. 지수 표기법은 과학적 표기법(Scientific Notation)이라고도 합니다. 지수 표기법은 아주 크거나 아주 작은 숫자들을 십진법으로 편하게 작성하여 표현하는 방법입니다. 예를 들어, 숫자 12345678901은 1.23E+10으로 표시하며, 이는 1.23 곱하기 10의 10제곱입니다. 지수 표기법은 숫자를 "-d.ddd…E+ddd" 또는 "-d.ddd…e+ddd" 형태의 문자열로 변환합니다. 여기서 각 "d"는 숫자(0-9)를 나타냅니다. 숫자가 음수이면 문자열 앞에 빼기 기호가 붙습니다. 정수를 한 자리만 표시하는 규칙을 가지고 있기에 소수점 앞에는 항상 숫자가 하나만 있어야 합니다.
- 실수E+지수: 실수 곱하기 지수만큼의 10의 거듭제곱을 나타냅니다.
- -3.4E+38: -3.4 곱하기 10의 38제곱입니다.
- 1.7E+308: 1.7 곱하기 10의 308제곱입니다.
6.10.2. C 언어 실수 데이터 타입 사용하기
소개
C 언어에서 기본으로 제공하는 실수 데이터 타입을 사용하겠습니다. C 언어에서 실수 데이터 타입은 float, double, long double의 키워드를 사용하여 소수점이 있는 실수 데이터는 저장할 수 있습니다. 특별한 경우가 아니면 박용준 강사의 강의에서는 double 형식을 기본으로 사용합니다.
실수 데이터 타입을 printf 펑션으로 출력할 때 서식 지정자는 다음과 같습니다.
float:%fdouble:%lf또는%f사용 가능long double:%Lf
코드: floating_point.c
// 실수 데이터 타입 사용하기
#include <stdio.h>
#include <float.h> // 실수 데이터 타입의 최댓값과 최솟값에 대한 상수 정의
int main(void)
{
//[1] 실수 데이터 타입 변수 선언
float f = 3.141592f; // 단정밀도 부동소수점 변수, 숫자 뒤에 f 접미사 붙임
double d = 3.141592; // 배정밀도 부동소수점 변수, 접미사를 붙이지 않음
long double ld = 3.141592l; // 배정밀도 부동소수점 변수 접미사 l을 붙임
//[2] 자리 표시자: float(%f), double(%f), long double(%Lf)
printf("%.6f %.6f %.6Lf\n", f, d, ld); // 3.141592 3.141592 3.141592
// 서식 지정자로 지수 표기법 사용: float(%e), double(%e), long double(%Le)
printf("%e %e %Le\n", f, d, ld); // 3.141592e+00 3.141592e+00 3.141592e+00
//[3] 실수 데이터 타입 크기: sizeof로 데이터 타입 크기를 알 수 있고 %llu로 출력
// 리눅스 환경의 GCC 컴파일러에서는 서식 지정자로 %llu 대신에 %lu로 출력해야 함
printf("%llu %llu %llu\n", sizeof(float), sizeof(double), sizeof(long double));
//[4] 실수 데이터 타입의 범위: 큰 숫자이므로 지수 표기법으로 출력
printf("float: %e ~ %e\n", FLT_MIN, FLT_MAX);
printf("double: %e ~ %e\n", DBL_MIN, DBL_MAX);
printf("long double: %Le ~ %Le\n", LDBL_MIN, LDBL_MAX);
return 0;
}
Windows에서 실행 결과
3.141592 3.141592 3.141592
3.141592e+00 3.141592e+00 3.141592e+00
4 8 8
float: 1.175494e-38 ~ 3.402823e+38
double: 2.225074e-308 ~ 1.797693e+308
long double: 2.225074e-308 ~ 1.797693e+308
Linux에서 실행 결과
3.141592 3.141592 3.141592
3.141592e+00 3.141592e+00 3.141592e+00
4 8 16
float: 1.175494e-38 ~ 3.402823e+38
double: 2.225074e-308 ~ 1.797693e+308
long double: 3.362103e-4932 ~ 1.189731e+4932
- [1] 실수 데이터 타입은 각각
float,double,long double키워드를 사용하여 데이터를 저장합니다. 이 때 실수 데이터는double키워드를 기본으로 사용하겠습니다. - [2] 실수 데이터 타입 출력에 대한 서식 지정자는
%f,%Lf를 기준으로%e,%Le형태로 지수 표기법으로도 표현이 가능합니다. - [3]
sizeof()연산자를 통해서 실수 데이터 타입의 크기를 구할 수가 있습니다. 여기서 주의할 것은 데이터 타입의 크기는 운영체제마다 다를 수 있습니다. - [4]
float.h헤더 파일에는 실수 데이터 형식의 최댓값과 최솟값을 담고 있는 상수가 정의되어 있습니다.FLT_MIN,FLT_MAX,DBL_MIN,DBL_MAX,LDBL_MIN,LDBL_MAX의 6개 상수로float,double,long double의 최댓값과 최솟값을 알 수 있습니다. 이것도 마찬가지로 운영체제마다 다를 수 있습니다.
6.10.3 실수 데이터 타입의 서식 지정자
이번 절에서는 복습을 통해 실수 데이터 타입의 서식 지정자를 다시 사용해 보겠습니다. 이 예제에서는 실수(float, double, long double) 데이터 형식을 출력할 때 사용되는 서식 지정자 %f, %e, %g를 적용해 보입니다.
코드: float_print.c
// float_print.c
// 실수 데이터 형식의 주요 서식 지정자 사용 예시
#include <stdio.h>
int main(void)
{
float weight = 70.5F; // float 형 변수
double pi = 3140E-3; // double 형 변수, 3140 * 10^-3, 즉 3.140
// 실수를 다양한 서식으로 출력
printf("weight: %.2f, %e => %g\n", weight, weight, weight);
printf("pi: %.2f, %e => %g\n", pi, pi, pi);
return 0;
}
실행 결과
weight: 70.50, 7.050000e+01 => 70.5
pi: 3.14, 3.140000e+00 => 3.14
여기서 %f 서식 지정자는 고정 소수점 표현을 사용하여 실수를 출력하고, 소수점 이하 두 자리(%.2f)로 제한합니다. %e는 지수 형식으로 실수를 표현하며, %g는 주어진 값에 따라 %f와 %e 중 보다 적합한 형식을 자동으로 선택하여 출력합니다. 이러한 서식 지정자들은 실수 값을 다양한 방식으로 표현할 때 유용하게 사용됩니다.
6.11. typedef 키워드로 새로운 형식 만들기
typedef 키워드를 사용하면 C 언어에서 기본으로 제공하는 int, float, double과 같은 키워드에 대한 새로운 별칭을 부여해서 사용할 수도 있습니다. 물론, 나중에 배울 구조체에서는 많이 사용되나 기본 제공 데이터 타입에 대해서는 많이 사용되진 않지만, 참고로 기억하세요.
typedef 키워드 별칭;
코드: type_def.c
#include <stdio.h>
int main(void)
{
typedef int number; // int 형식을 number 이름의 별칭으로 사용
number age = 123; // int age = 123; 코드와 동일
printf("%d\n", age);
return 0;
}
123
typedef 키워드로 int 키워드에 별칭을 number 키워드로 추가했습니다. 그러면 현재 프로그램내에서는 int와 number는 모두 int 형식의 변수를 선언할 수 있는 키워드로 사용이 됩니다.
Typedef 키워드 사용하기
typedef 키워드는 "type을 definition한다"의 의미를 가지며, 기존의 데이터 타입에 새로운 이름을 부여하는 별칭을 설정할 때 사용됩니다. 이를 통해 코드의 가독성을 향상시키고, 특정 데이터 타입을 프로젝트 전반에 걸쳐 일관되게 사용할 수 있도록 도와줍니다.
예를 들어, C 언어에서 double 타입을 number라는 새로운 이름으로 정의하여 사용할 수 있습니다.
코드: typedef_keyword.c
// typedef 키워드 사용하기
#include <stdio.h>
// double을 number라는 이름으로 정의
typedef double number;
int main(void)
{
number num1 = 1234.56; // 이는 double num1 = 1234.56;과 동일합니다.
printf("%.2lf\n", num1); // 출력: 1234.56
return 0;
}
실행 결과
1234.56
강의 자료
- 관련 동영상 강의를 보려면 여기를 클릭하세요: Typedef 키워드 사용법
동영상 강의는 typedef 키워드의 개념을 더 깊이 있게 설명하며, 실제 코드 예시를 통해 사용 방법을 자세히 보여줍니다.
진법 계산
C 언어에서 진법 계산은 주로 10진법, 8진법, 그리고 16진법 수를 다루는 데 사용됩니다. 이러한 수치 체계를 사용하는 이유는 컴퓨터 하드웨어와 프로그래밍에서 특정 형태의 데이터 표현이나 계산에 유리하기 때문입니다. 여기서 각 진법의 기본 개념과 C 언어에서의 사용 방법을 간략하게 설명합니다.
10진법 (Decimal)
- 가장 일반적인 숫자 체계로, 0부터 9까지의 숫자를 사용합니다.
- C 언어에서는 숫자를 기본적으로 10진법으로 해석합니다.
- 예:
int decimal = 10;
8진법 (Octal)
- 0부터 7까지의 숫자를 사용합니다.
- C 언어에서 8진법 수를 나타내려면, 숫자 앞에
0(영)을 붙입니다. - 예:
int octal = 024;// 024의 8진법은 10진법으로 20입니다.
16진법 (Hexadecimal)
- 0부터 9까지의 숫자와 A(10)부터 F(15)까지의 문자를 사용합니다.
- C 언어에서 16진법 수를 나타내려면, 숫자 앞에
0x또는0X를 붙입니다. - 예:
int hex = 0x2A;// 0x2A의 16진법은 10진법으로 42입니다.
진법 변환
진법 변환은 다른 진법의 숫자를 10진법으로 변환하거나 그 반대로 변환하는 과정을 말합니다. 8진법이나 16진법을 10진법으로 변환할 때는 각 자리수에 해당 진법의 거듭제곱을 곱한 후, 그 결과를 모두 더합니다.
예를 들어, 8진법 숫자 024를 10진법으로 변환하려면:
- (2 \times 8^1 + 4 \times 8^0 = 16 + 4 = 20)
16진법 숫자 0x2A를 10진법으로 변환하려면:
- (2 \times 16^1 + 10 \times 16^0 = 32 + 10 = 42)
C 언어에서 이러한 진법 표기는 주로 메모리 주소, 비트마스킹 연산, 특정 하드웨어의 레지스터 값을 설정할 때 유용하게 사용됩니다.
6.12. 장 요약
숫자 데이터 타입을 나타내는 키워드는 많이 있지만, 가장 많이 사용되는 것은 int, long, float, double입니다. 그리고 모든 숫자 데이터 타입은 최댓값과 최솟값을 제공하지만 범위를 외울 필요는 없습니다. 프로그램을 작성하면서 자연스럽게 각각의 범위에 맞는 데이터 타입을 사용하는 법을 익힐 수가 있습니다.
정보처리산업기사 실기 시험 기출 문제 - 진법 변환과 정수 연산
문제
다음 C 프로그램이 실행되었을 때의 동작을 설명하고, 출력 결과를 예측하시오.
소스 코드 파일명: number_systems_and_arithmetic.c
#include <stdio.h>
main()
{
int j = 024, k = 24, L = 0x24, hap;
hap = j + k + L;
printf("%d, %d, %d, %d\n", j, k, L, hap);
}
입력 예시
이 프로그램은 입력을 받지 않습니다.
출력 예시
20, 24, 36, 80
해설
이 프로그램은 다양한 진법을 사용하여 정수를 선언하고, 이들의 합을 계산한 후 출력합니다.
int j = 024;는 8진법으로 표현된 정수를 선언하고 있으며, 10진수로는 20입니다.int k = 24;는 10진법으로 표현된 정수를 선언하고 있으며, 그대로 24입니다.int L = 0x24;는 16진법으로 표현된 정수를 선언하고 있으며, 10진수로는 36입니다.hap = j + k + L;는 선언된 세 변수의 합을 계산합니다. 따라서20 + 24 + 36 = 80이 됩니다.printf("%d, %d, %d, %d\n", j, k, L, hap);는 각 변수의 값을 순서대로 출력합니다. 따라서 출력 결과는20, 24, 36, 80이 됩니다.
int j = 024;에서 024는 8진법(octal)으로 표현된 숫자입니다. 8진법에서 각 자리는 (8^0), (8^1), (8^2), ... 등의 가중치를 가지며, 가장 오른쪽 자리부터 0번째 자리로 칩니다.
024라는 8진법 숫자를 10진법으로 변환하려면, 각 자리의 숫자에 해당 자리의 가중치(8의 거듭제곱)을 곱한 뒤, 그 결과들을 모두 더해야 합니다.
여기서 024는 8진법이므로,
- 4는 (8^0) 자리에 있으므로, (4 \times 8^0 = 4)
- 2는 (8^1) 자리에 있으므로, (2 \times 8^1 = 16)
따라서, 024의 10진법 값은 (4 + 16 = 20)입니다.
int L = 0x24;에서 0x24는 16진법(hexadecimal)으로 표현된 숫자입니다. 16진법에서 각 자리는 (16^0), (16^1), (16^2), ... 등의 가중치를 가지며, 가장 오른쪽 자리부터 0번째 자리로 칩니다.
0x24라는 16진법 숫자를 10진법으로 변환하려면, 각 자리의 숫자(또는 알파벳이 나타내는 숫자 값)에 해당 자리의 가중치(16의 거듭제곱)을 곱한 뒤, 그 결과들을 모두 더해야 합니다.
여기서 0x24는 16진법이므로,
- 4는 (16^0) 자리에 있으므로, (4 \times 16^0 = 4)
- 2는 (16^1) 자리에 있으므로, (2 \times 16^1 = 32)
따라서, 0x24의 10진법 값은 (4 + 32 = 36)입니다.
이 프로그램은 8진법, 10진법, 16진법으로 표현된 정수들의 이해와 이들을 활용한 연산을 보여줍니다. 또한, 변수 간 연산 결과를 출력하는 방법을 설명합니다.